本文来自读者投稿，作者：黄同学

这是一篇关于推断统计、参数估计和假设检验等概念的全面讲解以及在python中的如何实现的文章，全文共5000字，建议收藏后阅读~

1、总体、个体、样本和样本容量

1）总体、个体、样本和样本容量的概念

• 总体：我们所要研究的问题的所有数据，称为总体。

• 个体：总体中的某个数据，就是个体。总体是所有个体构成的集合。

• 样本：从总体中抽取的部分个体，就构成了一个样本。样本是总体的一个子集。

• 样本容量：样本中包含的个体数量，称为样本容量。

2）本文章使用的相关python库

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
from sklearn.datasets import load_iris
from scipy import stats
sns.set(style="darkgrid")
mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore")

2、推断统计的概念

1）推断统计的概念

“推断统计”研究的是用样本数据去推断总体数量特征的一种方法。它是在对样本数据进行描述的基础上，对统计总体的未知数量特征做出以概率形式表述的推断。

2）为什么要进行推断统计？

在实际研究中，总体数据的获取往往是比较困难的，总体参数一般也是未知的。因此，我们就需要利用总体的某个样本，通过样本统计量去估计总体参数。基于这个需求，我们就需要学习推断统计。

通过上述叙述，我们给推断统计做一个说明。“推断统计”就是利用样本统计量，去推断总体参数的一种方法。
  

3、参数估计(点估计和区间估计)

1）参数估计、点估计和区间统计的概念

• 参数估计：用样本统计量去估计总体的参数。比如，用样本均值去估计总体均值，用样本方差去估计总体方差。

• 点估计：用样本统计量的某个取值，直接作为总体参数的估计值。

• 区间估计：在点估计的基础之上，给出总体参数估计值的一个区间范围，该区间通常由样本统计量加减估计误差得到。

2）点估计说明

① 怎么求鸢尾花的平均花瓣长度？

事实上，世界上鸢尾花千千万，我们总不能说把所有的鸢尾花的数据信息，都统计出来。因此，这就需要我们用样本均值去估计总体均值。

iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))
# 计算鸢尾花花瓣长度的均值
df["petal length (cm)"].mean()

结果如下：

结果分析：点估计有点简单粗暴，容易受到随机抽样的影响，很难保证结果的准确性。但是，点估计也不是一无是处，样本值是来自总体的一个抽样，在一定程度上还是可以反映出总体的一部分特征。同时，样本容量越接近总体容量，点估计值也会越准确。
  

3）区间估计说明

① 什么是区间估计？

当你碰到一个陌生人，我让你判断出这个人的年龄是多少？这里有两种方式完成你的推断。第一，这个人25岁。第二，这个人20-25岁之间。哪种结果更让你信服呢？很明显第二种更让人信服。对于第一种说法，相当于上述的点估计。第二种，相当于区间估计，就是给定一个区间，这个区间包含真值。

统计学中对区间估计的定义：在点估计的基础之上，给出总体参数估计的一个区间范围，该区间通常由样本统计量加减估计误差得到。

问题：获取一个抽样样本后，如何确定置信区间和置信度？

要确定置信区间和置信度，就需要知道样本和总体，在分布上有怎样的联系。中心极限定理给出了这个问题很好的回答。上述疑问将在下面为您一一揭晓。
  

4、中心极限定理

1）中心极限定理的概念

设从均值为μ，方差为σ²的任意一个总体中，抽取样本量为n的样本。当n充分大的时候，样本均值X拔近似服从均值为μ，方差为σ²/n的正态分布。

注意：中心极限定理要求n充分大，但是多大才叫充分大呢？一般在统计学中n>=30称之为大样本(统计学中的一种经验说法)。因此在实际生产中，不用多想，肯定都是大样本。

2）中心极限定理的推导(手写推导)

设X1,X1,…,Xn是从总体中抽取出来的样本容量为n的随机样本，假设总体均值为μ，方差为σ²。那么很显然这n个样本是独立同分布的，“独立”指的就是每个个体被抽到的概率是相同的，每个球被抽到也不会影响其它球被抽到，“同分布”指的是每一个个体都和总体分布一样，均值为μ，方差为σ²。

基于上述叙述，下面我们来推导样本均值X拔的分布。

3）由中心极限定理得出的几个结论

• 不管进行多少次抽样，每次抽样都会得到一个均值。当每次抽取的样本容量n足够大时，样本均值总会围绕总体均值附近，呈现正态分布。

• 当样本容量n足够大时，样本均值构成正态分布，样本均值近似等于总体均值μ，而样本方差等于总体方差σ²除以n，即σ²/n。

• 样本均值分布的标准差，我们称之为标准误差，简称“标准误”。

4）python实现中心极限定理

# 设置一个随机种子，保证每次产生的随机数都是一定的
np.random.seed(3)
# 产生均值为50，标准差为80，大小为100000的一个总体
all_ = np.random.normal(loc=50,scale=80,size=100000)
# 创建一个样本均值数组
mean_array = np.zeros(10000)
for i in range(len(mean_array)):
    mean_array[i] = np.random.choice(all_,size=64,replace=True).mean()

display("样本的均值：",mean_array.mean())
display("样本的标准差：",mean_array.std())
display("偏度：",pd.Series(mean_array).skew())
sns.distplot(mean_array)

结果如下：

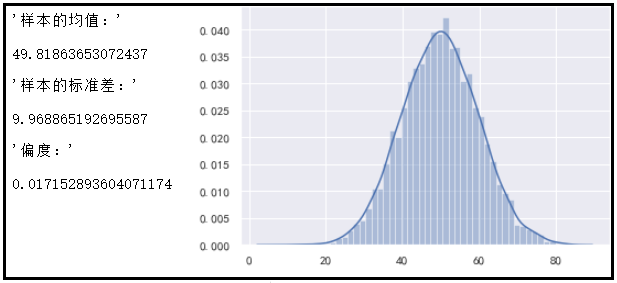
从图中可以看出：样本均值近似等于总体均值50，而样本方差等于总体方差80除以8，即10。

5、参数估计中置信区间的推导

我们要知道什么是α值，什么是置信度，什么是置信区间，以及怎么求置信区间。首先要了解以下几方面的知识，才能有一个比较透彻的了解。

1）什么是小概率事件？
2）随机变量的分布的概念。
3）标准正态分布的概率密度函数和和分布函数
4）随机变量的α分位数的概念。
5）标准正态的分位数表怎么得到的呢？
6）区间估计的概念。
7）置信水平1-α的解释
8）枢轴法求置信区间的步骤。

1）什么是小概率事件？

“小概率事件”指的就是在一次随机试验中，几乎不可能发生。
假定参数是射击靶上10环的位置，随机进行一次射击，打在靶心10环的位置上的可能性很小，但是打中靶子的可能性确很大。然后用打在靶上的这个点画出一个区间，这个区间包含靶心的可能性就很大，这就是区间估计的基本思想。

2）随机变量的分布的概念

3）标准正态分布的概率密度函数和和分布函数

4）随机变量的α分位数的概念

5）标准正态的分位数表怎么得到的呢？

① 标准正态分位数表的公式推导

② 标准正态分布分位数表

6）区间估计的定义

7）置信水平1-α的解释

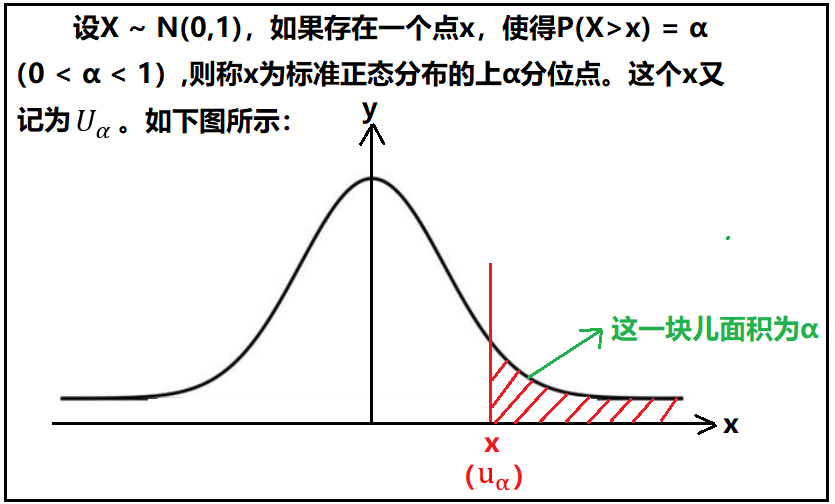
对总体样本进行反复抽样(每次抽取到的样本容量都为n)，那么每个样本均值都会确定一个区间(a,b)，每个这样的区间要么包含总体参数，要么不包含总体参数，不能说成“以多大的概率包含总体的参数”。其中包含总体参数的区间有1-α个，而只有α个区间不包含总体参数，如下图所示(红色表示该样本构成的区间估计不包含总体参数，白色表示该样本构成的区间估计包含总体参数)。

用一个详细的案例说明：如果对总体返回抽样10000次，每次抽样的样本量都是n，每个样本都会得到一个区间估计，那么10000次抽样，就会得到10000个区间。当置信水平1-α=95%时，那么就表示10000个区间中包含总体参数的有9500个抽样样本，只有500个样本不包含总体参数，这个不包含总体参数的样本就相当于我们估计错误。这个概率只有5%。这个5%在统计学中，就叫做小概率事件，也就是说在一次随机试验中，这个小概率事件不可能发生。

即：当我们随机抽取一个样本容量为n的抽样样本，并且利用这个样本构造总体参数的置信区间，当指定了置信水平1-α=95%时，那么这个样本，基本就可以认为是包含了总体参数，也就是说，总体参数就在这个置信区间内。

8）枢轴法求置信区间的步骤(手写推导)

① 什么是枢轴量？

• 枢轴量指的就是包含待估计参数，而不包含其它未知参数，并且分布已知的一个量。

• 枢轴量设计到三个重要点：1、包含估计参数。2、不包含其它未知参数。3、该枢轴量的分布已知。

②以总体μ的置信区间为例(方差σ²已知)，讲述枢轴量求置信区间的步骤。

6、假设检验

1）假设检验的概念

假设检验，也称为显著性检验，指通过样本的统计量，来判断与总体参数之间是否存在差异(差异是否显著)。我们事先对总体参数进行一定的假设，然后通过收集到的数据，来验证我们之前作出的假设(总体参数)是否合理。

在假设检验中，我们会建立两个完全对立的假设，分别为原假设H0与备择假设H1。然后根据样本信息进行分析判断，是选择接受原假设，还是拒绝原假设(接受备择假设)。假设检验基于“反证法”。首先，我们会假设原假设为真，如果在此基础上，得出了违反逻辑与常理的结论，则表明原假设是错误的，我们就接受备择假设。否则，我们就没有充分的理由推翻原假设，此时我们选择去接受原假设。

2）假设检验的理论依据(小概率事件)

在假设检验中，违反逻辑与常规的结论，就是小概奉事件。我们认为，#小概率事件在一次试验中是不会发生的*。我们首先认为原假设为真，如果在此基础上，小概率事件发生，则我们就拒绝原假设，否则，我们就选择去接受原假设。

假设检验遵循“疑罪从无”的原则，接受原假设，并不代表原假设一定是正确的，只是我们没有充分的证据，去证明原假设是错误的，因此只能维持原假设。那么，假设检验中的小概率事件是怎么得出的呢？想想之前讲到的置信区间，是不是一切都验然开朗了？

“疑罪从无”很形象的说明的假设检验向我们传达的含义。也就是说，当我们没有充分的理由拒绝原假设，就必须接受原假设，即使原假设是错误的，但是你找不到证据证明原假设是错误的，你就只能认为原假设是对的。反之，经过一次随机试验，你如果找到了某个理由拒绝了原假设，那么原假设肯定就是错误的，这个是一定的。

3）P-Value值与显著性水平

假设检验，用来检验样本的统计量与总体参数，是否存在显著性差异。那么如何才算显著呢？我们就可以计算一个概率值(P-Value)，该概率值可以认为就是支持原假设的概率，因为在假设检验中，通常原假设为等值假设，因此，P-Value也就表示样本统计量与总体参数无差异的概率。然后，我们再设定一个阈值，这个阈值叫做“显著性水平 ” (使用α表示)，通常α的取值为0.05(1-α叫做置信度)。当P-Value的值大于α时，接受原假设。当P-Value的值小于α时，拒绝原假设。简单记为：p值越小越拒绝原假设。软件中一般都会展示这个p值，那里的p值，指的就是我们这里所叙述的p值。

假设检验和参数估计是推断统计的两个组成部分，都是利用样本对总体进行某种推断，但是两者进行推断的角度不同。参数估计讨论的是用样本统计量估计总体参数的一种方法，总体参数在估计前是未知的。而假设检验，则是对总体参数先提出一个假设，然后用样本信息去检验这个假设是否成立。

4）假设检验的步骤

① 根据实际问题的要求，提出原假设和备择假设。
② 给出显著性水平α以及样本容量n。
③ 确定检验统计量和拒绝域。
④ 计算出检验统计量的值，并作出决策。

5）单边检验和双边检验

6）常用的假设检验

① 单个正态总体均值的假设检验法(Z检验：方差已知)

Z检验用来判断样本均值是否与总体均值具有显著性差异。Z检验是通过正态分布的理论来推断差异发生的概率，从而比较两个均值的差异是否显著。Z检验适用于：

• 总体呈正态分布。

• 总体方差已知。

• 样本容量较大。
  

  

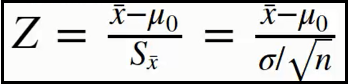
② 案例如下

③ 有个人说：鸢尾花的平均花瓣长度为3.5cm，这种说法可靠吗？假设经过长期大量验证，鸢尾花花瓣长度总体的标准差为1.8cm，我们就可以使用Z检验来验证了。

from scipy import stats

iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))

mean = df["petal length (cm)"].mean()
n = len(df)
sigma = 1.8

z = (mean - 3.5) / (sigma / np.sqrt(n))
display(z)

结果如下：

④ 单个正态总体均值的假设检验法(t检验：方差未知)

t检验，与Z检验类似，用来判断样本均值是否与总体均值具有显替性差异。不过，t检验是基于t分布的。检验适用于：

• 总体呈正态分布。

• 总体方差未知。

• 样本容量较小。
  

  

⑤ 案例说明

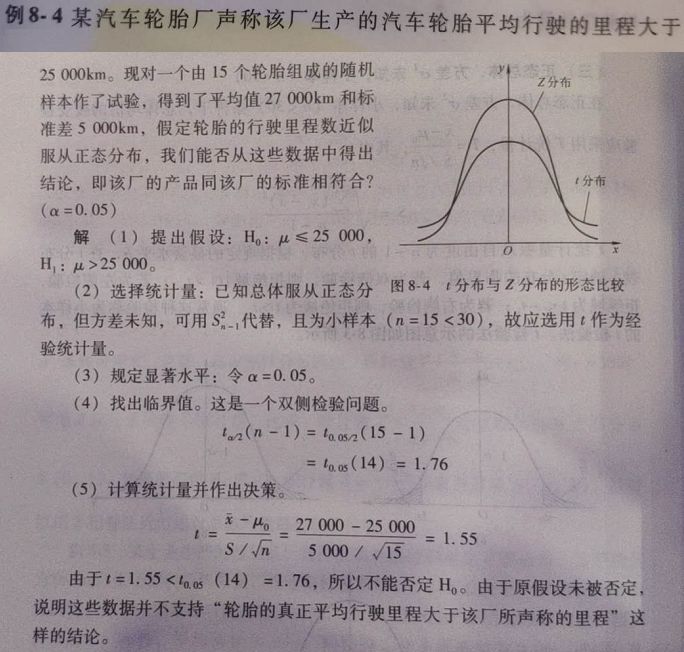
⑥ 代码演示

# 方法一
iris = load_iris()
dt = np.concatenate([iris.data,iris.target.reshape(-1,1)],axis=1)
df = pd.DataFrame(dt,columns=iris.feature_names + ["types"])
display(df.sample(5))

mean = df["petal length (cm)"].mean()
std = df["petal length (cm)"].std()
n = len(df)
display(mean,std)
t = (mean - 3.5) / (std / np.sqrt(n))
display(t)

# 方法二
from scipy import stats
stats.ttest_1samp(df["petal length (cm)"],3.5)

结果如下：

欢迎扫码关注作者的CSDN：

猜你喜欢：

快速提高Python数据分析速度的八个技巧

Python数据结构：字典那些事儿

可以用统计模型做决策吗

人生若只如初见：初识统计学

@ 号主：可乐

@ 公众号/知乎专栏/头条/简书：可乐的数据分析之路
@ 加微信（data_cola）备注：进群，拉你进可乐的数据分析交流群，每日数据分析知识总结，不定期行业经验分享